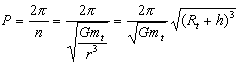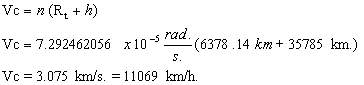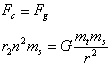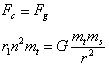|
Basic notions of
Celestial Mechanics
Mohamad Magdy
Abd El Rasoul
Egypt-kafr El
Shiekh -Balteem
Don’t worry
about your mathematical difficulties;
I assure you
that mine are greater !
Albert
Einstein
1. Law of
Universal Gravitation
As his friend Halley
was right in stating "Nec fas
est propius mortali attingere divos" - "No
mortal nearer the Gods could reach", we should feel when
studying the great genius of Sir
Isaac Newton.
His great contributions to
science, astronomy, optics, physics, the invention of Calculus and
marvelous geometric perception of the Universe make us remember the Alexander
Pope (XVIII century) poem, where in some place says "Nature
and nature’s laws lay hid
in night. God said 'let Newton be' and all was light".
The law of gravitation formulated
by Newton says "Each particle of
matter attracts any other particle of matter with a force proportional
to the product of their masses and inversely proportional to the square
of the distance between them". In the universal language
of mathematics, this can be stated as:
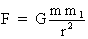
Where m and m1 are the masses of both particles, r is the distance between them, F is
the attractive gravitational force and G is the so-called constant of
universal gravitation.
The numeric value of
is 6.672 x 10-11 m3 kg-1s-2.
Before going any deeper in the
application of the law of universal gravitation and its relationship
with the planetary orbits, let us see an example of said law in the
circular orbits of the terrestrial artificial satellites
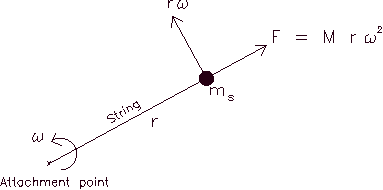
Figure 1.1
Figure 1.1 depicts a mass ms attached to the tip of a string which is being swung around a fixed point
with an angular velocity
. According to the dynamics of our
example, the mass experiences a direct action of the centrifugal force
which is proportional to the mass, its distance to the rotation point
and to the square of the angular velocity.
The resulting centrifugal force
is Fc = msr
2 and it is said to be in equilibrium with
the force made at the point of rotation, should not this be the case the
mass would be shot in a tangential trajectory to the circle of rotation.
Applying this example to a
satellite in rotation around the Earth we have that the force that keeps
the satellite in orbit is the force of gravity, which replaces the
string in our above example, and is proportional to the mass of the
Earth mt, the mass of the
satellite ms and inversely
proportional to the square of the distance between the center of the
Earth and the satellite.
Therefore, this force
Fg is expressed as:
1.1.
If we set this equation equal to
the corresponding centrifugal force, we have:
1.2
Equation 1.2
is the basis of the circular motion of a satellite in orbit around the
Earth. It is important to note that the mass of the satellite, in this
equation, can be cancelled as it appears in both sides and therefore if
we were to calculate the mass of a body, for instance that of the Earth,
the reference central body should be the Earth itself and not the
observed body.
From equation
1.2 we have:
1.3
Let us
introduce the concept of mean
movement n, instead of the angular velocity
. From equation 1.3 we have that said
mean movement is:
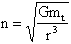1.4
The
instantaneous circular speed of the satellite is obtained by multiplying
each member of the equation by
r.
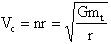1.5
Based in the
satellite speed around the Earth or the value of its mean movement we
can calculate the period of the satellite as the longitude of the arc
for a complete revolution is 2
r. Denoting the speed or our satellite
as Vc , the duration or a
revolution is:
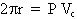1.6
where P is the
period, ie.
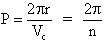1.7
Now, equation
1.5 allows us to deduce that the speed of a satellite can be determined
from the mass of the Earth, its distance and the constant of universal
gravitation.
As a matter of
fact, we can express the distance to the center of the Earth as the sum
of the height of the satellite and the radius of the Earth, as.
1.8
where Rt
is the equatorial Earth’s radius and h is the height or
elevation of the satellite above the surface of the Earth.
Based on the
above, we can transform equation 1.5 in:
1.9
As a practical
application we can study the case of the geostationary satellites, whose
orbits are placed about the plane of the equator and which allow the
transmission and reception of radio communication through very long
distances by means of parabolic antennas. The main parameter of these
satellites is that they always stay on the same spot in the sky, that is
why the satellites dishes are always fixed !. In this sense, their
period with respect to the fixed stars is 23h 56m., a concept closely
related to that of sidereal time.
Because this
period is 23h 56m or 86,160 seconds, their mean movement is:
From equations
1.4 and 1.7 we have:
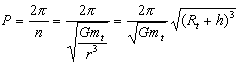; where we have replaced r by Rt +
h
From this last
equation we can deduce that the height h of the satellite is:
The numerical
values used are
for G,
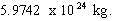for the Earth’s mass and 6378.14 km. for its radius.
The speed of
these satellites is obtained as:
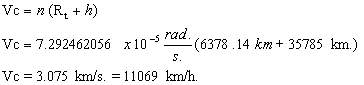
But going back
to our study if we square both member of equation 1.4 and multiply them
by r3, we obtain:
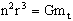1.10
This equation
is a very famous one in celestial mechanics and its a form of one of the
Kepler´s Laws which will be discussed below. In fact, equation 1.1 is
an approximation to the exact relationship as it does not consider the
mass of the satellite in respect to that of the central body. This
approximation, however, for the case or artificial satellites is
perfectly valid for all practical purposes.
Figure 1.2
Figure 1.2
allows us to derive the mentioned exact relationship if we suppose that
it represents the Earth and a satellite, two asteroids of similar mass
or a binary star system. In this figure r1 and r2
represent de distances of the bodies with masses m1 and m2
to their mutual center or mass.
For the case
of the Earth and an artificial satellite, we have m1= mt
y m2 = ms.
The system is
in static equilibrium if
For the
satellite:
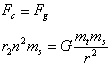1.11
and for the
Earth:
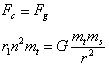1.12
If we cancel ms
from equation 1.11 and mt from
equation 1.12, and equal them we have:
1.13
By adding
equations 1.11 and 1.12 we
obtain:
|
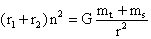
