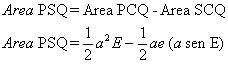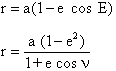|
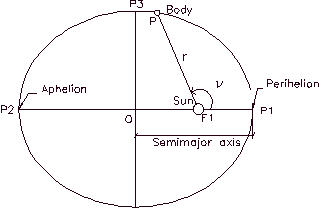
Figure 4.2 In figure 4.2 we have: OP1 = Semi-major axis, OP3
= Semi-minor axis, O = Center
of the ellipse
r
= Radius vector of the planet (Distance between the
centers of the Sun and the planet) n = true anomaly
of the body The basic geometry of a planetary
orbit is described by its semi-major axis (which determines its size)
and the eccentricity (which determines its shape). Let us recall that an
eccentricity of exactly 0 defines a circular orbit, of 1 a parabolic
orbit and larger than 1 a hyperbolic orbit. All planets follow
elliptical orbits and therefore their eccentricity have values between 0
and 1 (actually much less than 1). Orbital anomalies: There are three angles called
anomalies which allow us to determine the position of a planet around
the Sun on a given instant.
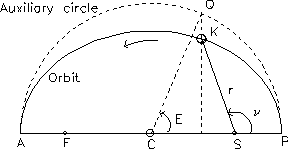
Figure 4.3 Referring to figure 4.3, let us
suppose that a given body is located at K on a given instant. Distance
SK is its distance to the Sun and as previously mentioned is know as its
radius vector, which it is .normally expressed in Astronomical Units (1
A.U. equals 149,597,870 km). The angle KSP is known as the true anomaly
(n) and is the
angle which the planet has swept, as seen from the Sun, since its last
passage by the perihelion (least
distance to the Sun) denoted by P on this figure. Also, consider an external
auxiliary circle PQA, whose diameter is 2a
and where Q is determined by th perpendicular through K to
the semi-major axis of the ellipse. Angle E is equal to PCQ and is known
as the eccentric anomaly.
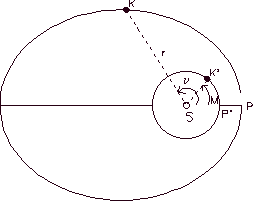
Figure 4.4 Let us now consider figure 4.4,
in which a fictitious body K' is moving around the Sun in a circular
orbit with constant speed and an orbital period equal
to that of the
real body K. If we suppose that the fictitious body is located at P' in
the instant that the real body it at its perihelion at P, then after a
given time the real body will be at K and the fictitious body will be at
K'. The angle PSK is the true anomaly (n) and the angle
PSK' is known as the mean anomaly M, which is the angle, measured from
the perihelion point, that the body would have swept if moving at a
constant speed. For a given value of the
eccentricity e, the
initial problem consists in finding the true anomaly (n) from the mean
anomaly M. The key to this problem is based in finding a solution for
the "equation of Kepler". This equation is
"simply" stated as: E = M + e sen E
4.10 Where the angles are expressed in
circular measure (ie. radians) As easily seen, equation
4.10 is of trascendental nature and cannot be solved analytically, but
rather is more easily solved using iterative or numerical methods. As
mentioned before, even as it looks rather simple, its solution has
always been a subject of interest
and careful study. However, as complex as it is, its
derivation is quite simple and can be done as follows: From figure 4.3 we have: By Kepler’s second law (law or
areas):
Also:
Now, we have that:
After some simple algebraic
manipulation, we obtain:
The true anomaly is related to
the eccentric anomaly and the eccentricity by the following formula:
Once the eccentric or true
anomalies have been found, the radius vector is easily calculated by one
of the following formulae:
References
-
Adventures in celestial
mechanics, V. G. Szebehely, University of Texas Press, 1991 -
Fundamentals of
Astrodynamics, Bate, Mueller and White, Dover Publications, 1971 -
Textbook of spherical
astronomy, W. Smart, Cambridge University Press, 1977 -
Solving Kepler´s equation
over three centuries, P. Colwell, Willmann Bell, Inc. 1993 -
An introduction to
celestial mechanics, F. R. Moulton, Dover publications Inc. 1970 -
Celestial mechanics – A
computational guide for the practitioner, L. G. Taff, John Wiley &
Sons, 1985 -
Fundamentals of celestial
mechanics, J.M.A. Danby, Willmann-Bell, Inc. 1988 |