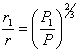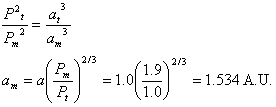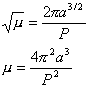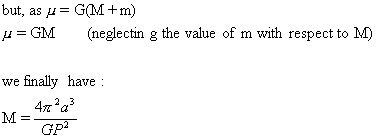Recalling from last chapter the expression for the mean movement  and introducing the value of  P in equation 4.4 we obtain:

                                                                                                4.5

Obviously, for each planet, this expression is constant and thus we have verified Kepler’s second law.

Additionally, when the planet moves from SP to SQ the radius vector sweeps an angle   in an interval of time t. At point P, the angular speed is  in  such a way that the mean movement n is the average value for  for all points along the orbit.

The third law, mathematically expressed is:

                                                                                                          4.6

where r and r1 are the semi-major axes of two planets and P and P1 are their respective orbital periods around the Sun.

  Recalling equation 1.4, we have:                                                           4.7

  Now, from equation 4.6, we have:

                                                                                                       4.8

By comparing equation 4.8, obtained from Kepler’s third law, with the exact relation found in equation 1.18 and after some Algebra, we can see that it is in fact a very good approximation and we really obtain the equation 1.19 previously discussed.

Now, let us recall equation 1.14, for the Sun-Earth system:

And for a system Sun-planet:

Combining these two equations, we obtain:

Introducing equation 1.7, we finally obtain:

                                                                                            4.9

  This last equation is the exact form of Kepler’s third law and we can see that the ratio  is very close to unity and thus in its original form reflects quite a good approximation to reality.

Graph 4.1

  It results rather interesting to compare, for each and every one of the planets, their semi-major axes against their orbital periods and construct a logarithmic graph with these parameters. It is obvious that because of the "perfect" alignment thus found this is a graphical way of proving the validity of Kepler´s third law for all planets in the solar system.

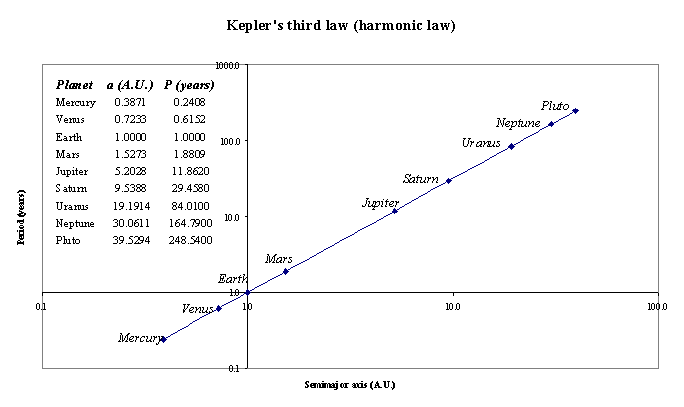
  Example 4.1.

 Determine the semi-major axis of Mars if by observation we know that its orbital period is 1.9 years.

  Introducing unit values for the Earth and using the approximate solution provided by equation 4.6 we have:

Example 4.2.

 Using the data from example 3.1 from chapter 3, let us calculate the mass of the Earth.

  Recalling equation 3.14:

  Now, solving for :

  Introducing the numerical value from example 3.1, we have:

  a = 7190.8 km , P = 1.684 hours

We have used for G :

The Equation of Kepler:

Of all of the trascendental equations found in celestial mechanics and mathematics in general, certainly few have generated so much study and interest as the equation of Kepler. Quoting F.R. Moulton in his book "An introduction to Celestial Mechanics" from 1914, we recall "A great number of analytical and graphical solutions have been discovered and almost all of the greatest mathematicians since Newton until the mid of last century have paid some of attention to the subject". Additionally, he mentions that an incomplete list from 1900 already had more than 123 papers about Kepler’s equation. In fact, there is a recent book dedicated exclusively to the description and solution by a large number of methods titled “Solving Kepler’s equation over three centuries” Peter Colwell, Willmann-Bell Inc., 1993.

Before we carry out the derivation of Kepler’s equation, we shall introduce the concept of orbital anomalies. These anomalies are simply auxiliary angles that allow us to locate a planet on a given time considering its movement along an ellipse with a determined eccentricity.

Geometry of the planetary orbits

As already thoroughly discussed and proven, planets move in elliptical orbits around the Sun. In this chapter we shall see several important parameters of the study of elliptical movement under the influence of gravity.