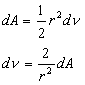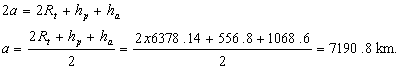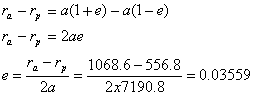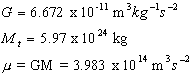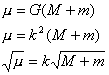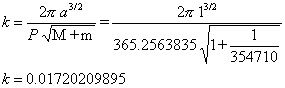|
Also, for an infinitesimal
triangular element, considering that both sides are equal we find that:
Which when replaced in equation
3.1, we obtain:
The
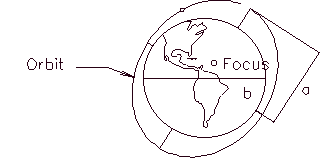
period and apocenter/pericenter distances
of the Explorer 7 satellite are 1.684 hours and
1068.6 kilometers and 556.8 kilometers respectively. Let us find
the semi-axes and eccentricity of its orbit, as well as its apocenter
and pericenter speeds.
Figure 3.4 By checking figures 3.1 and 3.4
is easy to see that twice the semi-major axis is equal to the sum of the
pericenter and apocenter distances plus the Earthís diameter, which
expressed as twice its radius, allows us to state:
The above result means that the
satelliteís speed while at its pericenter is just 7.4% greater than
its minimum speed at its farthest point from Earth, which of course is
due to its rather low level of eccentricity. Selection of units and the determination of the
gravitational constant of Gauss Let us define
Now, recalling equation 3.14, we
have:
In this sense, k
can be determined from equation 3.14 and choosing the appropriate units
of time, mass and distance. Although it is obvious that these can be
chosen arbitrarily, it is convenient to use units common to astronomy by
choosing the unit of time as the mean solar day, the Sunís mass as the
unit of mass and the semi-major axis of Earthís orbit as the unit of
distance. In this way, k
is known as the Gaussí constant as it was this great mathematician who
first defined it like this in his famous "Theoria
Motus". If M is the Sunís mass and m
the sum of the masses of the Earth and Moon, then:
Also, the sidereal period is
365.2563835 mean solar days. Therefore, using these numerical
values, equation 3.15 when solved for k
is:
The determination of Earthís
orbital period as well as its mean distance was not exactly determined
then an thus the Gaussí "constant" would not be exactly that
which be determined if modern and accurate values were used. Therefore,
with the purposes of maintaining consistency and avoiding practical
difficulties, the above mentioned value for k
is still used today and the unit of distance is modified in such a way
that k retains its
original value and a
is exactly 1. 4. The laws and
Equation of Kepler We now shall see Keplerís laws
and the very important and quite famous "equation
of Kepler", by
studying with some detail the elliptical movement of bodies through
space. In their most general form,
Keplerís laws are descriptions rather that explanations and as we
shall see are easily deduced from the law of universal gravitation. Keplerís laws are: 1. Planets move
in elliptical orbits, with the Sun located at one of the foci. 2. Planets
sweep equal areas in equal times. 3. The square
of the periods of the planets are proportional to the third power of
their distances to the Sun. The first law refers to the
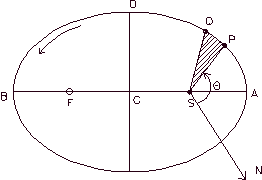
general geometry of the planetsí orbits around the Sun, as seen in
figure 4.1.
Figure 4.1 In the above figure, S and F are
the two foci and C is the center of the ellipse and AB is the major
axis. The Sun is located at S and the planet moves along the ellipse in
the indicated sense. When the planet is located at A it reaches the
least distance to the sun (Perihelion and reaches at B its farthest
distance to the Sun (Aphelion). The distance CA is the semi-major axis
of the orbit while CD is its semi-minor axis. The ratio between CS and
CA is the orbital eccentricity and as we have shown in previous chapters
defines the "shape" of the orbit. At a given point in time, the
distance between the planet and the Sun is called "radius vector" which of course is variable during
the planetís course around the Sun. The second law tells us that the
radius vector SP, in figure 4.1, sweeps out equal areas in equal times.
In order to see this, let us say that at a time t
a planet is located at P and then at a later time t +
t it is located at Q.
Now, at Q the radius vector is r +
r and
+
is the angle QSN. If the angle
is small enough, the arc QP can be
considered as a straight line and the area swept in an infinitesimal
time
t will simply be the area of the
triangle QSO, ie.
As
is taken very small, then the are can
be stated as
With respect to time, the rate of
change of the areas being swept by the planets, according to Kepler, are
constant therefore said change of speed is:
where h is
twice the sweeping rate of the areas with respect to time. We also know
that the area of the ellipse is ab
, where a and b are the
semi major and semi minor axes of the orbit. Now, the total area is
swept out, of course, in an interval of time P
(period of the orbit), thus:
From the
geometry of the ellipse (analytical geometry), the semi-minor axis can b
expressed in terms of the semi-major axis and the eccentricity as
follows:
Introducing
equation 4.3 in equation 4.2, we have:
|