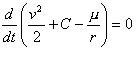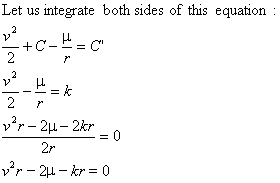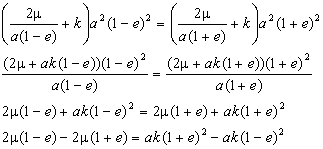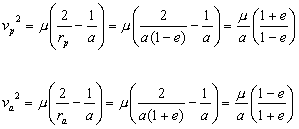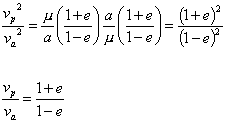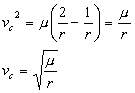3. Elliptical movement

 It is obvious that a comprehensive study of celestial mechanics must include a rigorous treatment of all possible orbital movement. However, as the main objective of this article is only to give a general impression of celestial mechanics without entering too much in its vast though beautiful complexities, we shall only discuss to some detail the elliptic orbits being the most general case and because all planets, Moon and satellites (both natural and artificial) follow this type or orbit.

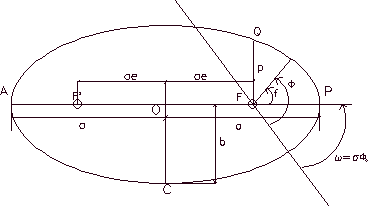
Figure 3.1

Through the use of basic analytic geometry, it is easy to show that:

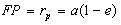   ; Pericenter distance (least distance to the central body                          3.1  

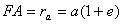; Apocenter distance (greatest distance to the central body)                    3.2

Because the distance from the center of ellipse to the foci is the product of the eccentricity and the semi-major axis.

Also, because of a property of the ellipse, we have that the semi-minor axis is: 

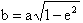
By virtue of equation 2.5 (conservation of the energy) we can deduce the velocity of a planet in an elliptic orbit, as follows:

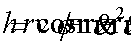       ;  Remember that  =G(M+m)

Going back a bit in the analysis that allowed us to deduce it, we have that:

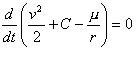
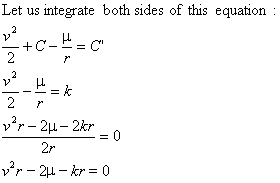
Therefore, we have that the speed of a body in elliptical motion is:

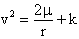                                                                                                       3.3

  Equation 3.3 is known as the Energy integral or also as the Vis-Viva integral.

  Now, the speed of the body at its pericenter and apocenter (through the use of equations 3.1, 3.2 and 3.3) are:

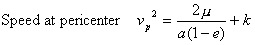                                                           3.4

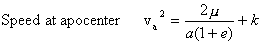                                                         3.5

  From the angular momemtum conservation law earlier proved, we can state that, due to the perpendicularity of the velocity and position vectors, that:

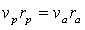                              (by equation  2.7A)                                           3.6

  Squaring both sides of this equation, we obtain:

  Introducing equations 3.4 and 3.5 we find:

  Which after some algebraic manipulation is equivalent to:

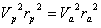
Finally:

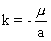                                                                                                              3.7           

  Based on the above, we can conclude then that the speed of a body in elliptic movement under the action of gravity is:

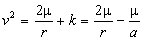
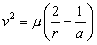                                                                                                   3.8.

  Also, from equation 3.8 we can easily calculate the speeds at pericenter and apocenter by recalling equations 3.1 and 3.2:

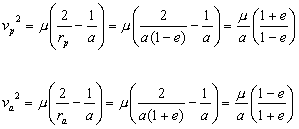                                                3.9

  The ratio of theoretical maximum (apocenter) and minimum (pericenter) speeds is found to depend solely on the eccentricity of the orbit, as follows:

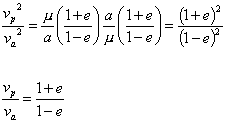
  If we know proceed to make a semi-logarithmic graph (figure 3.2) showing the above ratio for different value of the eccentricity we obtain a rather linear behavior up to an eccentricity of 0.8 and quite exponential from this point until right before 1.0 which from that point onwards the orbit will become open and cease to maintain a periodic movement.

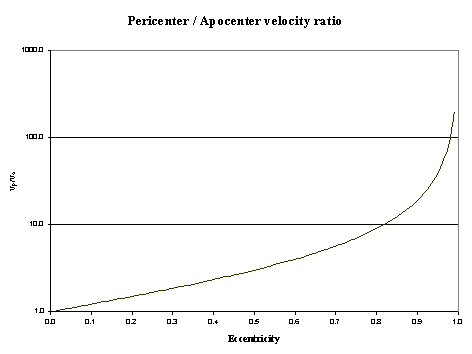
Figure 3.2

    For a circular orbit., ie. with zero eccentricity, its speed is directly calculated as:

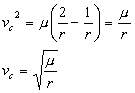                                                                                       3.10

It must be obvious to the reader that in this case the speed is constant for all values of r, being itself constant, and only depending on the mass of the body and that of its central body, without any exchange of energy.

Period of elliptic orbits

We can see in figure 3.3 that the horizontal component of the velocity of a body in elliptic movement is simply v cos , which can also be expressed as

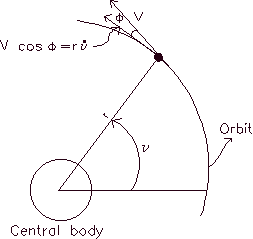
Figure 3.3

Recalling the angular momentum equation:

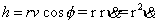
  we can state that:

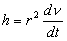
  Now, solving for dt, we obtain:

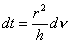                                                                                                         3.11