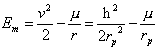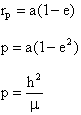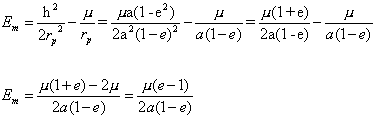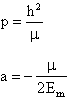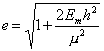|
Geometrical properties of the conic sections
We
have already seen how the bodies of our system follow conic orbits. In
this section we shall see what are exactly these orbits and discuss
briefly some of its properties.
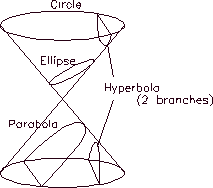
Figure 2.3
Conic sections have known since
ancient times and some of its more interesting characteristics were
widely known to the Greeks. Their name is a consequence of the fact that
any of the basic 4 curves can be generated by the intersection of a
plane (orbital plane !) and a right circular cone, as depicted in figure
2.3.
If said plane cuts only one of
the sections of the cone, then the generated curve will be an ellipse
which is the shape of all the orbits of the planets of the solar system.
In fact, the circle is a special form of the ellipse (with eccentricity
zero) and occurs when the intersection is parallel to the base of the
cone. One of the characteristics of these curves is that they a re
closed and that is why all bodies which follow elliptic orbits are
periodic and therefore remain orbiting the central body which governs
their motion.
If the plane is parallel to the
surface of the cone but only cuts one section, then the curve receives
the name of a parabola. This curve usually represents the orbits of many
Comets with the characteristic that being open such comets only come
once through the solar system. Although such comets can be captured by
the Sun or giant planets and become periodic as a consequence of
perturbational gravitational forces, but this a different problem
altogether.
If the plane cuts both sections
of the cone, then the curve
will be a Hyperbola with two branches. Although much less common, some
comets are know to follow this type of orbits which are also of open
shape.
From a mathematical point of
view, the conic sections can be defined as a curve in which the ratio
between the distance of a point, on the curve, to a fixed point, called
focus, and the absolute distance to a line called directix, is a
constant known as eccentricity.
Numerically, we have that if the eccentricity of a
conic is:
-
equal to 0, then the orbit/curve is a circle
-
greater than 0, but less than 1, then the orbit/curve is an ellipse
-
equal to 1, then the orbit/curve is a parabola
-
greater than 1, then the orbit/curve is a hyperbola
As mentioned above, all the
planets of the solar system follow elliptic orbits, being Venus that of
the least elongated orbit (near to zero) and Mercury that with the most
elongated orbit (highest eccentricity).
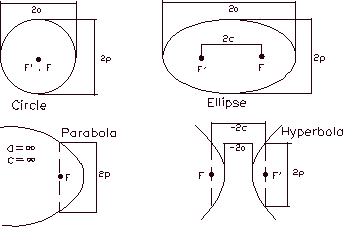
Figure 2.4
Figure 2.4 depicts all the family
of conic curves that can follow the celestial bodies under the effects
of the action of the force of gravity. Due to their symmetry, conics
have two foci, one of which is called the central focus and contains the
central body which governs the movement. The secondary focus is empty
and has no physical relevance in the study of the two body problem.
For the specific case of the
parabola, which marks the transition between the closed and open conics,
we can consider that said curve has the secondary focus located at an
infinite distance to the left of the central or main focus.
Additionally, we have that the
magnitude of the "span" of the curve, passing through the
focus, is twice the parameter of the conic (known as "latus
rectum") and is represented by 2p in the above figure.
The chord that passes though the
foci is called the major axis and is denoted by 2a in the figure. In the
circular orbits the major axis is nothing but the diameter of the orbit.
In the elliptic orbit is customary to use half of this dimension and is
then is know as the semi-major axis of the orbit. In the parabolic
orbits, the major axis is infinite as well as in the hyperbolic orbits,
although is considered as negative in the latter.
The distance between the foci is
depicted in figure 2.4 as 2c, and is zero for the circular orbits (for
having the foci coincident in the center of the orbit). For the
parabolic and hyperbolic orbits, this distance is considered to be
infinite.
For all conics, with the
exception of the parabola, we have:
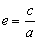 2.13
2.13
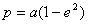 2.14
2.14
Relationship of the energy and angular momentum with the
geometry of the orbits
By studying equation 2.12 we can
conclude that the parameter of the conic depends solely on the angular
momentum and thus an increment in the angular momentum must have the
consequence of increasing the size of the orbit.
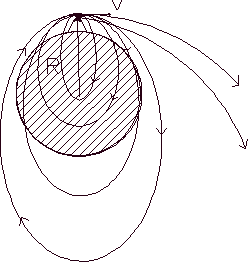
Figure 2.5
With the well-known analogy
(again due to Newton) depicted in figure 2.5, let us imagine a cannon
located in the summit of a mountain. If the angle of shot is zero (ie.
parallel to the horizon) then h=rv, because
is zero. By increasing the speed of the
bullet, thus increasing its energy, we will equivalently be increasing
the angular momentum.
In this figure we can observe the
family of curves that are generated by gradually increasing the
"angular momentum" and such curves are all of conic nature.
Conversely, we can also conclude that by increasing the angular momentum
we are effectively also increasing the parameter of the orbit, such as
stated by equation 2.12.
With the help this example we can
also deduce that at the pericenter (nearest point) or at the apocenter
(farthest point) of any orbit, the velocity vector is always tangential
to the orbit itself and therefore has a horizontal direction normal (ie.
perpendicular) to the position vector and thus as a corollary of
equation 2a we have:
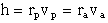 2.15
2.15
If we calculate the energy of the
orbit by means of equation 2.6 for the pericenter and using equation
2.15, we obtain:
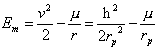
but we also know that:
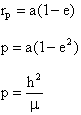
therefore:
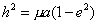
also, we have that:
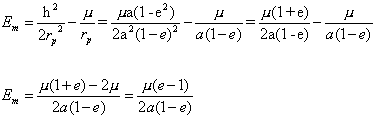
then, as a conclusion we can
state that:
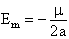 2.16
2.16
This quite simple relation, valid
for all conics, indicates us that the semi-major axis of an orbit
depends only on the energy of the orbiting body, which in turn depends
on the velocity and position of the body at a given point of the orbit.
Going back to figure 2.5, we can have a clearer picture of this
statement as we can see that by increasing the energy we are indeed
increasing the semi-major of its orbit.
Now, remembering figure 2.4 we
must bear in mind that the circular and elliptic orbits have their
semi-major axes defined as a positive quantity whereas it is considered
as infinite in the parabolic orbits and negative in the hyperbolic
orbits. This means, on the light of equation 2.16, that the specific
mechanic energy or a body in circular of elliptic orbits is negative,
zero for parabolic orbits and positive for hyperbolic orbits.
Additionally, as
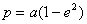 , we have that
, we have that
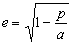
but,
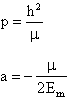
Therefore, we can conclude that
for any conic:
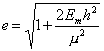 2.17
2.17
Studying this equation we can see
that if the energy is negative then the eccentricity is positive and
numerically less than one, ie. and ellipse. If the energy is zero, then
the eccentricity is numerically equal to one, ie. a parabola. Finally,
if the energy is positive then the eccentricity will also be positive
but numerically greater than one and therefore the orbit will be
hyperbolic.
It is also important to note that
in case that the angular momentum h
is zero, independently of the energy of the orbit, then the eccentricity
will be exactly one, but not really a parabola but rather a so-called
degenerate conic represented by a straight line or a point is space.
Conclusions:
Once all the above mathematical
analyses have been done, we can state with some rigor the following
important conclusions:
1.
The family of curves called "conic sections" (circle, ellipse,
parabola and hyperbola) represent the only possible curves that a
celestial body can follow while orbiting another one under the force of
gravity.
2.
The focus of an orbit is locates in the center of mass of the central
body which in turn governs the movement.
3.
The mechanic energy, ie. the sum of the kinetic and potential energy,
does not suffer modifications during the movement of the bodies.
However, there exists an exchange between the kinetic and potential
energies which means that the orbiting body must decrease its velocity
as its distance increases and that its velocity increases as its
distance to the central body decreases.
4.
The orbital movement is confined to a fixed plane
5.
The angular momentum of a body in orbit around a central body remains
constant
6.
The energy of the orbit of a body, regardless or its geometry, allows us
to determine the type and shape of the conic orbit over which the
secondary body orbits the central body
7.
The angular momentum is directly related to the geometry of the orbit
|